In part one of this series, I wrote about choosing a multi-tenant design for your software system. Let's now look at the different ways of achieving this.
Assume you have a unified code base for all tenants. One approach to support multiple tenants is to do a static switching. This mean, have some compile/deployment time controls or flags to choose the the tenant, and all class bindings and paths in your code are now restricted to the given tenant. This is a simplistic approach that works well for a small level of scalability. However, as you can see, this forces you to make a separate deployment for each tenant. As the number of customers increase, you will need to linearly increase the support team size to manage the deployments. On the plus side, you have a setup that needs no changes to your existing design. You can also run different versions of the product for different clients (instead of versioning the APIs, maintaining backward compatibility etc.). While this is not a good thing from the point of view of the engineering and ops teams, it is sometimes unavoidable, especially in a B2B setting.
A more involved solution is to dynamically decide, for each request, the tenant that is in play. This design is very flexible, simplifies the code base management (eventually) and paves way for cost optimization. There is however an upfront cost to set this all up and slightly increases the operational complexity (not something a bit of good devops and automation can't solve though). The best part of this approach is its flexibility - you could do a separate deployment for one tenant if required, or you could combine them too.
Let's see how flexible the second approach is during deployment. Say you decide to use kubernetes, you could choose separate namespaces for each tenant on same cluster (in which case, it is isolated from the software perspective, while your hardware, k8s versions, etc. are all shared), or you could have separate clusters altogether. You could also have one single namespace for all tenants (in a true multi-tenant way).
You could also do a completely shared deployment with compute and data stores (databases, message queues, storage etc.) all being the same for multiple tenants. This is the way to go for B2C software, because typically clients can sign up on their own. B2B is way different. A client might be concerned about data being stored in (or outside of) a particular country. They might ask that their data not be shared with other clients, at least logically, and that is what makes you keep all these options open.
Degrees of multi-tenancy
As we can see, there are varying degrees of multi-tenancy. From completely isolated software and hardware deployments to fully shared models. As always, it's something in between that typically ends up being the most practical one.
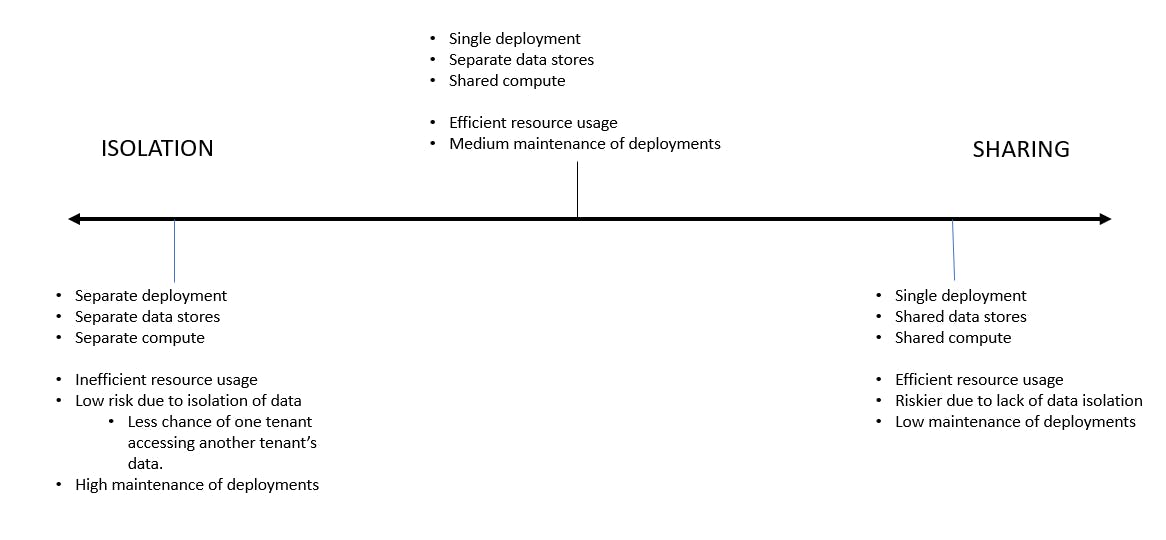
Sharing only compute among tenants is a great way towards multi-tenancy, because you gain all the good things like simplicity of operations and cost reduction. How quickly you achieve this depends on how your software is written.
Stateless services are key to moving towards this goal. Is there a shared state in your service? Static or global variables? Singletons? In-memory cache perhaps? When the same service is supposed to handle requests from multiple tenants, you cannot have any shared state, unless you make it tenant-aware.
What about object pools or connection pools? If you have shared compute, but separate databases, your connection pools also have to be tenant aware.
Distinguishing the tenant for each request is paramount when compute is shared. We can distinguish the tenant for each request using some middleware, where we use either the host name or maybe the access token of the logged-in user to determine the tenant. You then use it for figuring out the context for each execution.
Functional Testing and Automation is important when you go for multi-tenancy. You cannot afford to perform manual testing on each tenant for each change.
Another important aspect of sharing compute is to perform load testing to find correct auto-scaling options. Not only do you need to load test multiple tenants concurrently, you also need to set resource requests and limits in k8s appropriately.
Cover Photo by Quinton Coetzee on Unsplash

